用語解説
地盤破壊解析
極限平衡法
破壊が発生するときのすべり面の形と位置を決め、極限平衡状態におけるすべり面に沿う土塊の滑動力(すべり面に沿うせん断力)と土塊の持つ抵抗力(せん断強さ)を計算して斜面の安全性を求めるものです。この場合は、強度の異方性や進行性破壊現象を特に考慮せず、平均的な強度定数の選び方や安全率Fsですべり面上のひずみ分布を把握していないことをカバーする手法がとられています。
安定している斜面は極限平衡状態ではないため、斜面の安定解析ではすべり面上でのせん断強さを減じて仮想的な極限平衡状態を創り出しています。
安定している斜面は極限平衡状態ではないため、斜面の安定解析ではすべり面上でのせん断強さを減じて仮想的な極限平衡状態を創り出しています。
安全率
どの位すべり面の強度を減らしたら極限平衡状態になるかという目安になるのが安全率Fsです。つまり、土塊の極限せん断抵抗Sを安全率Fsで除すことによって、静定化するための仮定条件の中でスライスに関する力の多角形を閉合させています。
τ=S/Fs
S:極限せん断抵抗力
τ:せん断応力
Fs:安全率
必要安全率
Fellenius法(簡便法)
極限平衡法による安定計算は、すべり土塊をスライスに分割し、各スライスについて力の釣り合いを考えることになりますが、各スライスには図に示すように9個の力が作用しているのに対し、釣り合い式はX、Y方向の2式しかたてられないため、高次の不静定問題となって容易には解けません。
簡便法は、スライス側面に働くスライス間力Eはすべり面と平行で等しく、鉛直応力Vは作用しない(Fsに大きな影響を与えない)と仮定して、極限平衡法を用いて行う安定計算で、円弧すべりを対象にしています。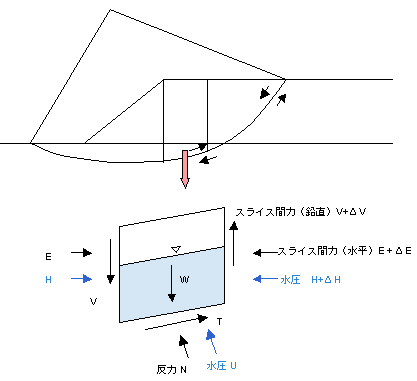 この式の中でΔH=0とおいた式を、簡便法(Fellenius法)と呼んでいます。
この式の中でΔH=0とおいた式を、簡便法(Fellenius法)と呼んでいます。
簡便法は、スライス側面に働くスライス間力Eはすべり面と平行で等しく、鉛直応力Vは作用しない(Fsに大きな影響を与えない)と仮定して、極限平衡法を用いて行う安定計算で、円弧すべりを対象にしています。

Fs=MR/MD
=Σ(C・L+(N?U)tanΦ)/Σ(W・sinα+ΔH・cosα)
=Σ{(C・L+(W・cosα?ΔH・sinα?U)tanΦ)}/Σ(W・sinα+ΔH・cosα)
ここで
C:すべり面の粘着力
L:すべり面の長さ
修正Fellenius法
Fellenius法は、すべり面の傾斜角αが大きくなると摩擦抵抗が負になる可能性があり、一般に過少な安全率を与えるという問題点が明らかになったため、静水圧分布地下水条件で、過剰間隙水圧が発生しないか、または過剰間隙水圧を考慮しない全応力解析の場合、(W・cosα?U)を浮力を差し引いた有効重量W´としました。
いずれにしろ、Fellenius法(修正Fellenius法)はスライス側面力に関する大胆な仮定を導入することによって問題の静定化に成功していますが、結果的には側面力を無視しています。
Fs=MR/MD
=Σ(C・L+W´・cosα・tanΦ)/Σ(W・sinα)
Bishop法(厳密法)
Bishopが1955年に「斜面の安定解析におけるすべり円弧の適用」でスライス間力を考慮した円弧すべりを対象にした安定解析法を提案したのが最初です。
上式を満足するFsおよびΔVを試行的に探す(スライスの和をとった時に0となるように設定)ことによって、次式よりスライス間力ΔEを求めます。(水圧ΔHは既知)また各スライスのモーメントが釣り合っていることから、スラスト線の位置を確定することができます。
Fs=(1/ ΣW・sinα)Σ[C・b/cosα+tanφ{W+ΔV ?U・cosα}
×secα/{1+(tanφ・tanα/Fs)}]
ここで b:スライス片の幅
Bishop法(簡易法)
Bishop法(厳密法)は1次の不静定問題となるため、唯一の解とはなりません。したがって、ΔV=0と置き、右辺の安全率の初期値(例えば1.0)を試行的に代入して左辺の安全率を求める方法を反復することによって、左辺の安全率を一定値に近づける方法を「厳密法」と区別して「Bishopの簡易法」と呼んでいます(通常Bishop法とはBishopの簡易法のことです)。
逆算法
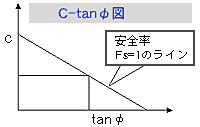
逆算法(C-tanφ図法)とは、すべり断面が与えられたものとして、これにある間隙水圧uのもとでの安全率Fsを推定(活動中の場合はFs=0.95?1.0の範囲で設定)して与え、これから逆算してすべり面でのせん断強度C、φを推定する方法です。この方法の場合、C-tanφ図上のどの点を選ぶかが問題となりますが、通常は最深のすべり面深さをh(m)とした場合に、それの1/10に相当する値をもってC(N/m^2)とし、このCとこれに対応するtanφをもって設計定数とする便法です。

有限要素法(Finite Element Method)
有限要素法は、解析対象である構造物や地盤を有限個数の要素に分割し、構造物や地盤全体の挙動を要素の集合体としての挙動におきかえ応力・変形解析を行う数値解析法です。
有限要素法では土の挙動を線形弾性体、非線形弾性体、弾塑性体などとして、理論の体系を組むことが可能です。歴史的に眺めると有限要素法は線形弾性体を対象に発展してきました。そのためか、有限要素法は変形を求めるのには適していますが、破壊状態に近い現象を扱うには適さないという意見がありました。しかし、計算手法の改良、工夫により有限要素法によっても十分破壊解析が行えるようになってきています。
有限要素法では土の挙動を線形弾性体、非線形弾性体、弾塑性体などとして、理論の体系を組むことが可能です。歴史的に眺めると有限要素法は線形弾性体を対象に発展してきました。そのためか、有限要素法は変形を求めるのには適していますが、破壊状態に近い現象を扱うには適さないという意見がありました。しかし、計算手法の改良、工夫により有限要素法によっても十分破壊解析が行えるようになってきています。
有限要素法による斜面安定評価法
有限要素法では、解析の結果として各要素毎に応力値が定まるため、下式の要素安全率(局所安全率)を定義して、その分布から解析系の安定性を評価するのが一般的です。
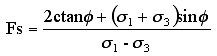 しかし、この手法では適切な荷重漸増載荷により、潜在すべり面の発生と進展を推察できる反面、地盤材料の構成則や解析手法によっては解析者に高度の判断力を要求されます。そこで、渡辺(フィルダムの動的解析に基づく安定評価手法の一考察:電力中央研究所報告381020,1981年12月)は、地盤内の連続した潜在円弧すべり面上土塊のすべり安全率を慣用的な分割法すべり計算と対比して次式のように定義しました。
しかし、この手法では適切な荷重漸増載荷により、潜在すべり面の発生と進展を推察できる反面、地盤材料の構成則や解析手法によっては解析者に高度の判断力を要求されます。そこで、渡辺(フィルダムの動的解析に基づく安定評価手法の一考察:電力中央研究所報告381020,1981年12月)は、地盤内の連続した潜在円弧すべり面上土塊のすべり安全率を慣用的な分割法すべり計算と対比して次式のように定義しました。
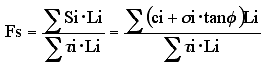 有限要素法を用いたすべり安全率Fsは、すべり面が通過する全ての要素の総和をとります。 慣用的な分割法すべり計算では、安全率Fsが構造系の静定化のために全分割片で一定と仮定しているのに対し、有限要素法を用いたすべり安全率Fsはすべり面上要素安全率の重み付き平均的な意味合いを持っています。
有限要素法を用いたすべり安全率Fsは、すべり面が通過する全ての要素の総和をとります。 慣用的な分割法すべり計算では、安全率Fsが構造系の静定化のために全分割片で一定と仮定しているのに対し、有限要素法を用いたすべり安全率Fsはすべり面上要素安全率の重み付き平均的な意味合いを持っています。
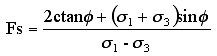
σ1,σ2:最大、最小主応力
C ,φ :粘着力と内部摩擦角
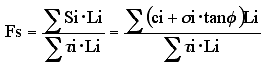
σi:要素iのすべり面上の直応力
τi:要素iのすべり面上のせん断応力
要素iのすべり面上の応力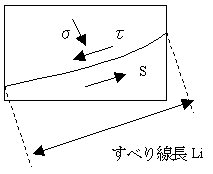

線形弾性解析
連続体力学では、釣り合い式と適合条件(全体的な変形と局所的な変形の間の関係式)および構成則が基本になっています。
 この中で、線形弾性解析は、応力σとひずみεの関係が一対一の対応にあるモデルを用いています。
この中で、線形弾性解析は、応力σとひずみεの関係が一対一の対応にあるモデルを用いています。

非線形弾性解析
非線形弾性とは弾性係数E、νが応力やひずみのレベルによって変化するもので、地盤材料の非線形挙動を表す最もシンプルな表現といえます。
地盤材料の非線形弾性表示式には種々のものが提案されていますが、それらの中で最も一般的に用いられているのは、Duncanらによる双曲線モデル(Duncan?Changモデル)と林らの提案による破壊接近度法、およびBi-Linearモデルがあります。
地盤材料の非線形弾性表示式には種々のものが提案されていますが、それらの中で最も一般的に用いられているのは、Duncanらによる双曲線モデル(Duncan?Changモデル)と林らの提案による破壊接近度法、およびBi-Linearモデルがあります。
弾塑性解析
圧縮量を弾性圧縮量と残留(塑性)圧縮量の和で表される性質を持つ物体を弾塑性体といいますが、弾塑性解析は弾性理論(フックの法則)と塑性理論(降伏曲面、硬化則、流れ則)を用いて弾性ひずみと塑性ひずみ増分を算出し、応力・変形特性を検討するものです。
逆算法で用いる現況安全率析
逆算法で用いる現況の安全率は、地すべりの分類や運動形態によって以下のように仮定されています。
【現況の安全率】
岩盤地すべり
風化岩地すべり
崩積土地すべり
粘質土地すべり
運動停止中
1.10
1.05?1.10
1.03?1.05
1.00?1.03
滑動中
0.99
0.95?0.99
0.93?0.95
0.90?0.93
摩擦力と粘着力
斜面の安定を考える場合には、摩擦力と粘着力の理解が重要になります。
摩擦には、内部摩擦と外部摩擦があり、内部摩擦はある特定の厚さの層のなかで生ずる摩擦のことで、これに対して外部摩擦はあいだに何もはさまない、物と斜面との摩擦です。さらに、静摩擦と動摩擦という区別もありますが、斜面の安定を考える場合の摩擦は、あくまで静摩擦のことを指すのが一般的です。ちなみに動摩擦は静摩擦の半分から2/3程度です。
摩擦力は、摩擦面にはたらく垂直力に比例し、見かけの接触面積の大小には関係しません。したがって、摩擦面に水膜がある場合は、水膜内に圧力が生じ荷重を支持するので摩擦力が低下します。一般に地すべり地には自由地下水や被圧地下水があるため、これらの水圧(間隙水圧)が浮力としてはたらき、安定に大きな影響を与えています。
一方、粘着力は簡単にいえば粘り気のことで、接触面にはたらく垂直力には無関係で、接触面積に比例します。
従来、逆算法では地すべり土塊の層圧の1/10をすべり面の粘着力と仮定して計算しますが、この粘着力をすべり面の物性と考えるのは根本的には誤りです。もし粘着力だけで安定を保っている斜面があるとして、この斜面においてたとえ地下水が地表まであったとしても、安定には何ら関与していないことになります。
摩擦には、内部摩擦と外部摩擦があり、内部摩擦はある特定の厚さの層のなかで生ずる摩擦のことで、これに対して外部摩擦はあいだに何もはさまない、物と斜面との摩擦です。さらに、静摩擦と動摩擦という区別もありますが、斜面の安定を考える場合の摩擦は、あくまで静摩擦のことを指すのが一般的です。ちなみに動摩擦は静摩擦の半分から2/3程度です。
摩擦力は、摩擦面にはたらく垂直力に比例し、見かけの接触面積の大小には関係しません。したがって、摩擦面に水膜がある場合は、水膜内に圧力が生じ荷重を支持するので摩擦力が低下します。一般に地すべり地には自由地下水や被圧地下水があるため、これらの水圧(間隙水圧)が浮力としてはたらき、安定に大きな影響を与えています。
一方、粘着力は簡単にいえば粘り気のことで、接触面にはたらく垂直力には無関係で、接触面積に比例します。
従来、逆算法では地すべり土塊の層圧の1/10をすべり面の粘着力と仮定して計算しますが、この粘着力をすべり面の物性と考えるのは根本的には誤りです。もし粘着力だけで安定を保っている斜面があるとして、この斜面においてたとえ地下水が地表まであったとしても、安定には何ら関与していないことになります。
斜面の傾斜と安全率
斜面の安定は、斜面の傾斜と関係が深く、安定勾配(安全限界角度)のおおよその見当をつけるには周辺の自然斜面の傾斜を観察することが、精密な計算を行うより重要です。斜面の傾斜は、底辺の長さと高さの比(高さ/底辺:tanФ)で、安全限界角度が45°とした場合、60度の安全率を簡易に算出すると、FS=tan45/tan60=1/1.732=0.57となります。
斜面の傾斜が急になればなるほど危険性が増大することは常識的なことですが、かならずしも傾斜がゆるいからといって安全になるとはかぎらない場合があります。この場合の主な原因は、雨水の浸透の問題で、斜面が急であるほど単位面積あたりの浸透する雨量がすくなくなるためで、九州のしらす地帯や厚い砂岩層地帯および外国では中国の黄土地帯などでは斜面の傾斜が急なほうが安全となります。
斜面の傾斜が急になればなるほど危険性が増大することは常識的なことですが、かならずしも傾斜がゆるいからといって安全になるとはかぎらない場合があります。この場合の主な原因は、雨水の浸透の問題で、斜面が急であるほど単位面積あたりの浸透する雨量がすくなくなるためで、九州のしらす地帯や厚い砂岩層地帯および外国では中国の黄土地帯などでは斜面の傾斜が急なほうが安全となります。
崩壊発生時期の予測
りや斜面の崩壊は、外力が破壊強度を上まわった場合でも、クリープをたどって破壊に至るため、実際の崩壊までには時間がかかります。クリープと破壊時間の間には一定の関係が成立しているとされていますが、この関係から破壊や崩壊の予測を行っている場合が一般的です。
崩壊発生時期の予測は、旧国鉄時代の斉藤迪孝・上沢弘の論文(1966)が出発点で、当時人工降雨による斜面崩壊実験の結果をまとめたものです。
斉藤迪孝は、定常クリープのひずみ速度と破壊時間との間に下図のような関係を見出しました。機器観測により定常ひずみ速度が分かれば、第3次クリープ段階に入ってからの破壊時間が予測できます。
log tr'=2.33-0.916log(ε×104)±0.59
また、斉藤は第3次クリープ領域で、ひずみ速度と崩壊までの余裕時間に逆比例関係があることを見出しました。
ε=Clog(t-t0)/( tr -t)
ε:ひずみ速度、tr :破壊時間、t0:基準時間、C:定数
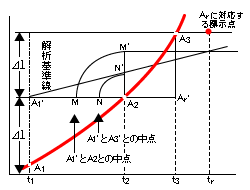
未知数が3個だから、クリープ曲線上の3点の座標値から破壊時間trが求められます。
下図の図式解法が簡便で、計算式は次式で与えられます。
tr-t1={1/2(t2-t1)2}/{(t2-t1)-1/2(t3-t1)}
崩壊発生時期の予測は、旧国鉄時代の斉藤迪孝・上沢弘の論文(1966)が出発点で、当時人工降雨による斜面崩壊実験の結果をまとめたものです。
斉藤迪孝は、定常クリープのひずみ速度と破壊時間との間に下図のような関係を見出しました。機器観測により定常ひずみ速度が分かれば、第3次クリープ段階に入ってからの破壊時間が予測できます。
log tr'=2.33-0.916log(ε×104)±0.59
また、斉藤は第3次クリープ領域で、ひずみ速度と崩壊までの余裕時間に逆比例関係があることを見出しました。
ε=Clog(t-t0)/( tr -t)
ε:ひずみ速度、tr :破壊時間、t0:基準時間、C:定数
未知数が3個だから、クリープ曲線上の3点の座標値から破壊時間trが求められます。
下図の図式解法が簡便で、計算式は次式で与えられます。
tr-t1={1/2(t2-t1)2}/{(t2-t1)-1/2(t3-t1)}

